With every weekly thread about glass shape, I am always trying to understand how shape impacts what we perceive. With the cool designs introduced on Berserker Day, and another ongoing thread on the next design in that series, I wanted to try and see if I could come up with something quantitative that might offer some explanation of why people prefer one glass over another (I had already started noodling on this a few weeks ago, Berserker Day just spurred me to get it done). So this is just the musings of a now retired science guy, who no longer has a lab to do real work in, so spends time generating what may or may not be useless data lol.
Thinking about what people look for in a glass, the conventional wisdom usually circles around volume, and “funneling aromas”. Frankly, some of this conventional wisdom has always seemed a little backward to me: A larger bowl should in theory need more volatiles to “fill it up”, and reach the opening. I’ve scratched my head to come up with some ways to quantitate this, and the three metrics I end up with are 1) volume of the space above the liquid surface, 2) surface area of the surface (possibly to include some increased area exposed by swirling), and 3) the height of the opening above the surface. There are others, like the size of the opening (though, as you’ll see, diameter at the lip of most conventional glassware is remarkably similar), but these are the easiest to model.
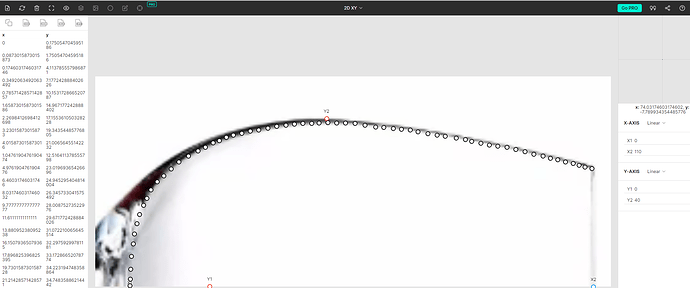
I chose a range of glass shapes, not trying to pick on anyone, but because they offered detailed shape and size info that I needed. For each shape, I used this web site PlotDigitizer Online App to manually “digitize” the outline of the glass, like this:
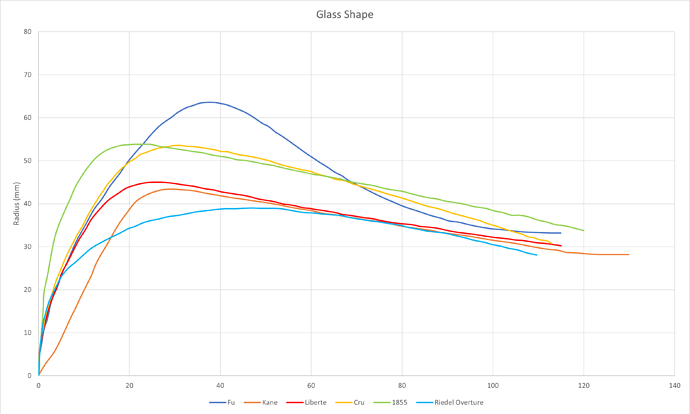
Here are all the shapes. I used Fu and Kane’s Glassvin shapes, three Grassl shapes, and the Riedel Overture, which is a glass I often use for wine dinners because it’s fairly small.
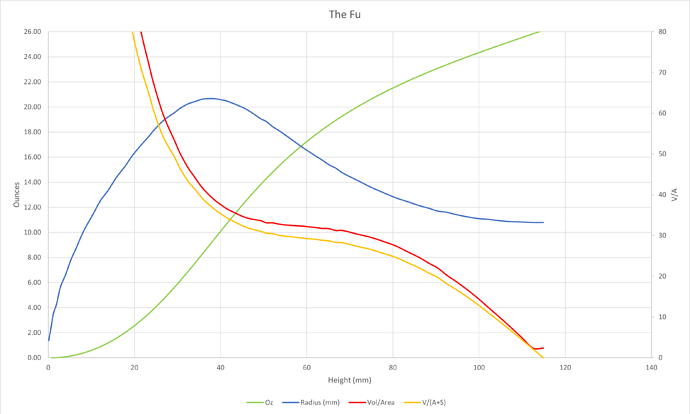
Dumped the shape data for each glass into Excel, and did some calculating: Volume of the air space as a function of fill level, surface area at different fill levels, height above the surface to the rim as a function of fill level, etc. From that, I derived the ratio of air space volume to surface area (which should be some measure of how much volume volatile compounds have to occupy, and the surface area from which they can escape). I wondered what happens when you swirl wine in your glass, so made an effort to compute the additional surface exposed to swirling wine, assuming you swirl gently about 2 cm above the static liquid level. Here’s what that data looks like for @CFu 's Berserker Day glass:
These graphs are plotted vs fill height, which is one way to look at it, though later I use ounces of fill along the X-axis, which I think is easier to think about. Blue is the shape, green is the fill volume. Yellow is the ratio of empty volume above the surface, to surface area of the static liquid, and red adds the swirl area to that static area. You can see that there isn’t a big difference in the added surface area from swirling (red vs. yellow curves). Let’s come back to how to interpret the yellow and red curves.
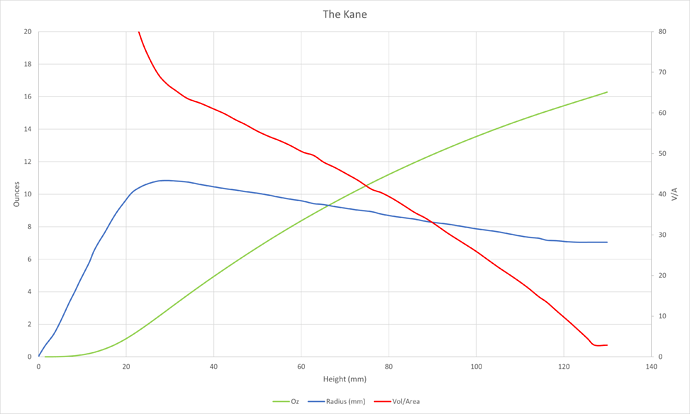
Here’s a similar plot of the Berserker Day “Kane” glass @K_John_Joseph
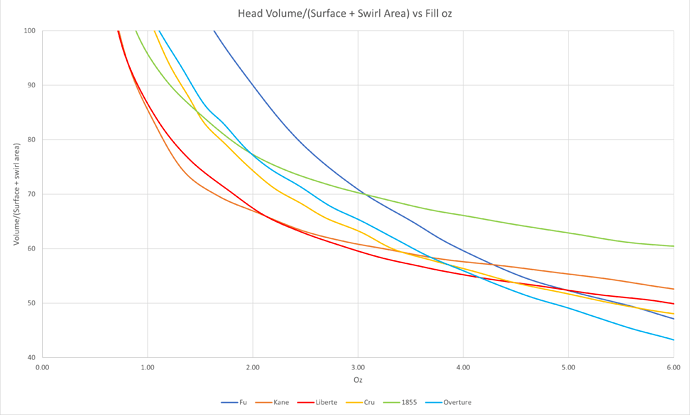
What does it all mean? It’s a little hard to say. I guess conventional wisdom would say you want the ratio of air volume to liquid surface area to be a smaller number. The trouble is, that number depends strongly on how full the glass is. With just a little wine in the bottom, it literally shoots off the charts. As you fill with more wine, that ratio drops, and the shape of that drop depends on the shape of the glass. The more extreme shape of the Fu glass is followed by the more extreme shape of the Volume/Area ratio, though note that with a modest 2 oz pour, or a typical 4 oz pour, the ratio is pretty high in the Fu. Maybe this isn’t the right metric? I don’t know, it’s what I was able to come up with.
Here’s the graph of volume/area ratio for all the glass shapes:
The big takeaway, for me, is that the metric changes a lot as you drink from the glass. For every shape, once you start drinking and lowering the fill level, that glass, in theory, gets worse and worse. My second conclusion, at least based on this metric, is that larger volume glasses are not necessarily “better”. They have a larger volume for volatile compounds to expand into, and the exposed surface area doesn’t increase proportionally. With the caveat that this is just one way to look at it.
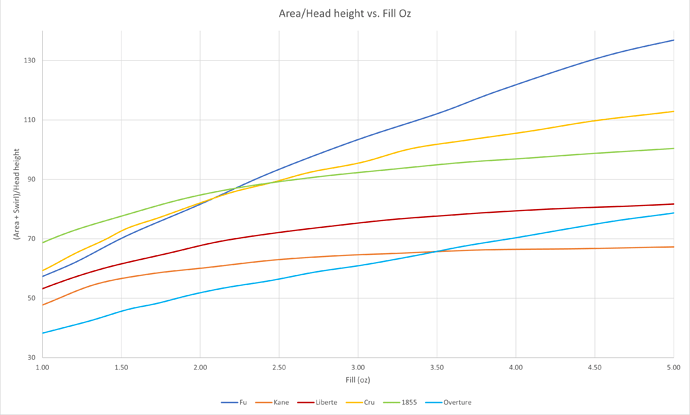
I’ve also wondered if a big factor in how we perceive a wine is not so much glass shape (apart from the psychological factor), but simply how far the wine is from your nose, i.e., the height of the opening above the liquid level. And for grins, I assume there is some benefit to how much surface area is exposed. I plotted that ratio of surface area to height:
Here, I’ll postulate you want a bigger number. Larger surface area for volatiles to escape from, and a smaller distance for them to travel to get out of the glass, and into your nose. For that, The Fu excels, and other larger bowl shapes also do well; while the taller, skinnier shapes like Liberte have smaller ratios, and a really small glass like the Overture comes out on the bottom, in the 2-4 oz range where we typically drink.
So there you have it, my contribution to the confusion of glass shapes 
Not meant to be definitive in any way, just one way to look at things.
Even gas molecules take quite a while to diffuse across a space, in the absence of any bulk motion (a breeze, a hand waving nearby, or pushing air around during the swirling motion). In a completely static glass of wine, volatile compounds will take up to several minutes to transit from the surface to the lip, depending on exactly how far that is, and how big the molecules are. When you pick up the glass, you push air around inside the bowl; when you swirl, that effect is even stronger. It’s a complex problem, and my little graphs can only go so far to describe it.
